Locating your Nook Inc. getaway package.

I’ve been playing Animal Crossing: New Horizons lately, where my in-game character flew to a deserted island in order to start a new life. Despite its cartoony art style, the game manages to establish a remarkable degree of realism, to the point where it almost feels like a living and breathing world. For example, I know for a fact that my island exists somewhere in the northern hemisphere; I know that the sun rises and sets there every real-world day; I know that the season shifts and spring is coming. At some point, I began to wonder how much further I can push this, e.g., given what’s observable in the game, can I deduce where my island is? If so, where might it be?

In this post, please join me for a tour to my island, and I will unveil its location at the end (sort of).

The Longitude

This is an easy one. Due to the fact that the game runs on real-world clock, my deserted island has to be conveniently located in the same time zone as where I physically am (or at least wherever my system is set). Voila! There it is and it can’t be too far off.

The Latitude

Unlike the previous case, figuring out the latitude can get a little tricky. In a nutshell, it boils down to measuring the solar elevation angle at solar noon. Astronomy tells us that the following equation holds true:

\[h = 90^\text{o} - \left| \phi - \delta \right|\]

where

• $h$ is the solar elevation angle at solar noon. It is also the angle between a ray of sunlight and the horizon at the observation point and can be found by taking inverse tangent on the ratio of the height of an object over the length of its shadow. In addition, solar noon is defined as the time of the day when the Sun reaches the highest point. Note that this is equivalent to the length of shadow being the shortest, and it doesn’t necessarily coincide with 12 pm.
• $\phi$ is the latitude of the observation point (a positive number in this case)
• $\delta$ is the latitude of the subsolar point (a negative number in this case)

For full reference, see here, here and here.

There’s yet one more challenge before we can pull this off in Animal Crossing. Because of the distortion introduced by the camera perspective, it’s not always obvious when the shadow of an object reaches its minimum in the game. That is, until you can afford a playground gym.

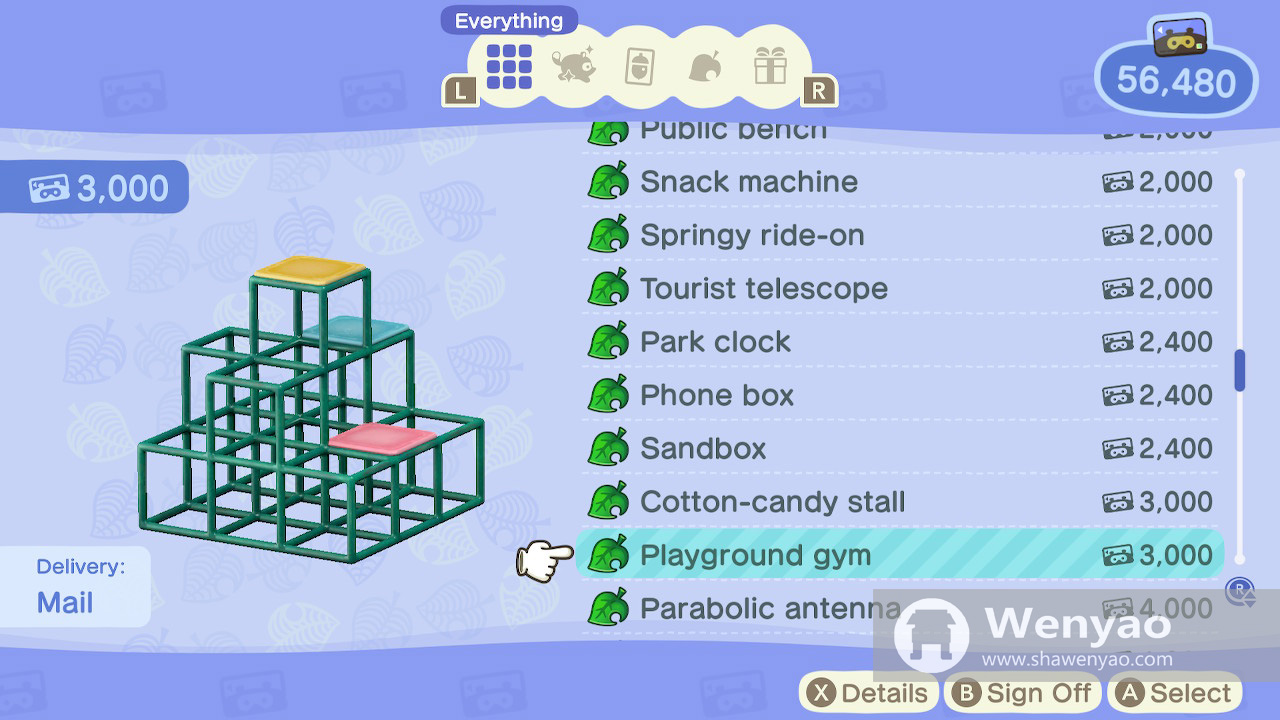
This baby will set you back 3000 Nook Miles, but oh boy is it worth every penny. Since I am reasonably confident that it’s made of little cubes, the playground gym forms some kind of orthonormal basis in a three-dimensional coordinate system when being placed on the ground, allowing distance to be estimated reliably on a relative basis.

The rest is straightforward but definitely not trivial. While my in-game character was enjoying his time on the swing, I ended up doing all the heavy lifting myself -

• capture the gameplay footage every two minutes or so around noon
• measure the height of an object as well as the minimal length of its shadow (a street lamp suits perfectly for this exercise)
• derive the solar elevation angle $h$.

\[h = \arctan{ \frac{ 4.9079 } { 3.5735 } } = 53.9412 ^\text{o}\]

From here, I know where the Sun is today (April 9th, 2020) which means $\delta$ equals $+7.9^\text{o}$. At last, the latitude of my island is given by:

\[\phi = 90^\text{o} - h + \delta = 43.9588 ^\text{o}\]

Putting It All Together

Now we get to observe where my island is on the globe, and in the absence of further evidence, I tend to believe that it also applies to the rest of the Animal Crossing players who happen to share the same northern hemisphere with me (i.e., same latitude but different longitude). Still, I am absolutely appalled to find that I am literally within 0.5 degree away from where the prediction says in terms of latitude.

But there’s a minor problem. There isn’t any island there!

This is Part I of my Animal Crossing post series. For Part II, see here.